Free Articles: Physical force

Force

For other uses, see Force (disambiguation).

Classical mechanics
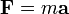$\mathbf{F} = m \mathbf{a}$ Newton's Second Law
History of classical mechanics · Timeline of classical mechanics

Force
SI symbol:	F
SI unit:	newton
Derivations from other quantities:	F = m·a

In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity (which includes to begin moving from a state of rest), i.e., to accelerate, or which can cause a flexible object to deform. Force can also be described by intuitive concepts such as a push or pull. A force has both magnitude and direction, making it a vector quantity. Newton's second law, F=ma, was originally formulated in slightly different, but equivalent terms: the original version states that the net force acting upon an object is equal to the rate at which its momentum changes.

Related concepts to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque which produces changes in rotational speed of an object. Forces which do not act uniformly on all parts of a body will also cause mechanical stresses, a technical term for influences which cause deformation of matter. While mechanical stress can remain embedded in a solid object, gradually deforming it, mechanical stress in a fluid determines changes in its pressure and volume.

Development of the concept

Philosophers in antiquity used the concept of force in the study of stationary and moving objects and simple machines, but thinkers such as Aristotle and Archimedes retained fundamental errors in understanding force. In part this was due to an incomplete understanding of the sometimes non-obvious force of friction, and a consequently inadequate view of the nature of natural motion. A fundamental error was the belief that a force is required to maintain motion, even at a constant velocity. Most of the previous misunderstandings about motion and force were eventually corrected by Sir Isaac Newton; with his mathematical insight, he formulated laws of motion that were not improved-on for nearly three hundred years. By the early 20th century, Einstein developed a theory of relativity that correctly predicted the action of forces on objects with increasing momenta near the speed of light, and also provided insight into the forces produced by gravitation and inertia.

With modern insights into quantum mechanics and technology that can accelerate particles close to the speed of light, particle physics has devised a Standard Model to describe forces between particles smaller than atoms. The Standard Model predicts that exchanged particles called gauge bosons are the fundamental means by which forces are emitted and absorbed. Only four main interactions are known: in order of decreasing strength, they are: strong, electromagnetic, weak, and gravitational. High-energy particle physics observations made during the 1970s and 1980s confirmed that the weak and electromagnetic forces are expressions of a more fundamental electroweak interaction.

Pre-Newtonian concepts

Newtonian mechanics

Newton's first law

Newton's second law

Newton's third law

Descriptions

Equilibria

Equilibrium occurs when the resultant force acting on a point particle is zero (that is, the vector sum of all forces is zero). When dealing with an extended body, it is also necessary that the net torque in it is 0.

There are two kinds of equilibrium: static equilibrium and dynamic equilibrium.

Static equilibrium

Dynamical equilibrium

Special relativity

In the special theory of relativity mass and energy are equivalent (as can be seen by calculating the work required to accelerate an object). When an object's velocity increases so does its energy and hence its mass equivalent (inertia). It thus requires more force to accelerate it the same amount than it did at a lower velocity. Newton's second law

$\vec{F} = \mathrm{d}\vec{p}/\mathrm{d}t$

remains valid because it is a mathematical definition. But in order to be conserved, relativistic momentum must be redefined as:

$\vec{p} = \frac{m\vec{v}}{\sqrt{1 - v^2/c^2}}$

where

v

is the velocity and

c

is the speed of light.

The relativistic expression relating force and acceleration for a particle with constant non-zero rest mass $m\,$ moving in the $x\,$ direction is:

$F_x = \gamma^3 m a_x \,$

$F_y = \gamma m a_y \,$

$F_z = \gamma m a_z \,$

where the Lorentz factor

$\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}.$

Relativistic force does not produce a constant acceleration, but an ever decreasing acceleration as the object approaches the speed of light. Note that $γ$ is undefined for an object with a non zero rest mass at the speed of light, and the theory yields no prediction at that speed.

One can however restore the form of

$F^\mu = mA^\mu \,$

for use in relativity through the use of four-vectors. This relation is correct in relativity when $F$ is the four-force, m is the invariant mass, and $A$ is the four-acceleration.

Feynman diagrams

Fundamental models

Gravity

Electromagnetic forces

Nuclear forces

Non-fundamental forces

Some forces are consequences of fundamental. In such situations, idealized models can be utilized to gain physical insight.

Normal force

Friction

Tension

Elastic force

Continuum mechanics

Fictitious forces

Rotations and torque

Centripetal force

Kinematic integrals

Potential energy

Conservative forces

Nonconservative forces

For certain physical scenarios, it is impossible to model forces as being due to gradient of potentials. This is often due to macrophysical considerations which yield forces as arising from a macroscopic statistical average of microstates. For example, friction is caused by the gradients of numerous electrostatic potentials between the atoms, but manifests as a force model which is independent of any macroscale position vector. Nonconservative forces other than friction include other contact forces, tension, compression, and drag. However, for any sufficiently detailed description, all these forces are the results of conservative ones since each of these macroscopic forces are the net results of the gradients of microscopic potentials.

The connection between macroscopic non-conservative forces and microscopic conservative forces is described by detailed treatment with statistical mechanics. In macroscopic closed systems, nonconservative forces act to change the internal energies of the system, and are often associated with the transfer of heat. According to the Second Law of Thermodynamics, nonconservative forces necessarily result in energy transformations within closed systems from ordered to more random conditions as entropy increases.

Units of measurement

The SI unit of force is the newton (symbol N), which is the force required to accelerate a one kilogram mass at a rate of one meter per second squared, or kg·m·s. The corresponding CGS unit is the dyne, the force required to accelerate a one gram mass by one centimeter per second squared, or g·cm·s. A newton is thus equal to 100,000 dyne.

The gravitational foot-pound-second English unit of force is the pound-force (lbf), defined as the force exerted by gravity on a pound-mass in the standard gravitational field of 9.80665 m·s. The pound-force provides an alternative unit of mass: one slug is the mass that will accelerate by one foot per second squared when acted on by one pound-force.

An alternative unit of force in a different foot-pound-second system, the absolute fps system, is the poundal, defined as the force required to accelerate a one pound mass at a rate of one foot per second squared. The units of slug and poundal are designed to avoid a constant of proportionality in Newton's second law.

The pound-force has a metric counterpart, less commonly used than the newton: the kilogram-force (kgf) (sometimes kilopond), is the force exerted by standard gravity on one kilogram of mass. The kilogram-force leads to an alternate, but rarely used unit of mass: the metric slug (sometimes mug or hyl) is that mass which accelerates at 1 m·s when subjected to a force of 1 kgf. The kilogram-force is not a part of the modern SI system, and is generally deprecated; however it still sees use for some purposes as expressing jet thrust, bicycle spoke tension, torque wrench settings and engine output torque. Other arcane units of force include the sthène which is equivalent to 1000 N and the kip which is equivalent to 1000 lbf.

Notes

References

Corbell, H.C.; Philip Stehle (1994). Classical Mechanics p 28,. New York: Dover publications. ISBN 0-486-68063-0.
Cutnell, John d.; Johnson, Kenneth W. (2004). Physics, Sixth Edition. Hoboken, NJ: John Wiley & Sons Inc.. ISBN 041-44895-8.
Feynman, R. P., Leighton, R. B., Sands, M. (1963). Lectures on Physics, Vol 1. Addison-Wesley. ISBN 0-201-02116-1.
Halliday, David; Robert Resnick; Kenneth S. Krane (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9.
Parker, Sybil (1993). Encyclopedia of Physics, p 443,. Ohio: McGraw-Hill. ISBN 0-07-051400-3.
Sears F., Zemansky M. & Young H. (1982). University Physics. Reading, MA: Addison-Wesley. ISBN 0-201-07199-1.
Serway, Raymond A. (2003). Physics for Scientists and Engineers. Philadelphia: Saunders College Publishing. ISBN 0-534-40842-7.
Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.
Verma, H.C. (2004). Concepts of Physics Vol 1. (2004 Reprint ed.). Bharti Bhavan. ISBN 81-7709-187-5.

External links

Retrieved from : http://en.wikipedia.org/w/index.php?title=Force&oldid=464652468

Free Articles

2011-12-25

Physical force