Log-Cauchy distribution
Probability density function | |
Cumulative distribution function | |
| parameters: | μ (real) (real) (real) |
|---|---|
| support: | 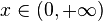 |
| pdf: | ![{ 1 \over x\pi } \left[ { \sigma \over (\ln x - \mu)^2 + \sigma^2 } \right], \ \ x>0](http://upload.wikimedia.org/wikipedia/en/math/5/6/d/56d668c2e57e844b62fb06645565fdbf.png) |
| cdf: |  |
| mean: | does not exist |
| median: |  |
| variance: | infinite |
| skewness: | does not exist |
| ex.kurtosis: | does not exist |
| mgf: | does not exist |
In probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution. If X is a random variable with a Cauchy distribution, then Y = exp(X) has a log-Cauchy distribution; likewise, if Y has a log-Cauchy distribution, then X = log(Y) has a Cauchy distribution.
Characterization
Probability density function
The log-Cauchy distribution has the probability density function:
where μ is a real number and σ > 0. If σ is known, the scale parameter is e. μ and σ correspond to the location parameter and scale parameter of the associated Cauchy distribution. Some authors define μ and σ as the location and scale parameters, respectively, of the log-Cauchy distribution.
For μ = 0 and σ = 1, corresponding to a standard Cauchy distribution, the probability density function reduces to:
Cumulative distribution function
The cumulative distribution function (cdf) when μ = 0 and σ = 1 is:
Survival function
The survival function when μ = 0 and σ = 1 is:
Hazard rate
The hazard rate when μ = 0 and σ = 1 is:
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.
Properties
The log-Cauchy distribution is an example of a heavy-tailed distribution. Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a Pareto distribution-type heavy tail, i.e., it has a logarithmically decaying tail. As with the Cauchy distribution, none of the non-trivial moments of the log-Cauchy distribution are finite. The mean is a moment so the log-Cauchy distribution does not have a defined mean or standard deviation.
The log-Cauchy distribution is infinitely divisible for some parameters but not for others. Like the lognormal distribution, and Weibull distribution, the log-Cauchy distribution is a special case of the . The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the Student's t distribution with 1 degree of freedom.
Since the Cauchy distribution is a stable distribution, the log-Cauchy distribution is a logstable distribution. Logstable distributions have poles at x=0.
Estimating parameters
The median of the natural logarithms of a sample is a robust estimator of μ. The median absolute deviation of the natural logarithms of a sample is a robust estimator of σ.
Uses
In Bayesian statistics, the log-Cauchy distribution can be used to approximate the improper Jeffreys-Haldane density, 1/k, which is sometimes suggested as the prior distribution for k where k is a positive parameter being estimated. The log-Cauchy distribution can be used to model certain survival processes where significant outliers or extreme results may occur. An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with HIV virus and showing symptoms of the disease, which may be very long for some people. It has also been proposed as a model for species abundance patterns.
References
Retrieved from : http://en.wikipedia.org/w/index.php?title=Log-Cauchy_distribution&oldid=460445189
![\begin{align} f(x; \mu,\sigma) & = \frac{1}{x\pi\sigma \left[1 + \left(\frac{\ln x - \mu}{\sigma}\right)^2\right]}, \ \ x>0 \\ & = { 1 \over x\pi } \left[ { \sigma \over (\ln x - \mu)^2 + \sigma^2 } \right], \ \ x>0 \end{align}](http://upload.wikimedia.org/wikipedia/en/math/3/a/0/3a0b1f973c315cd1a44f52d27de95b98.png)



